波动光学
相干光
光波相干的条件:
- 频率相同
- 相位差恒定
- 振动方向相同
注意:两个普通光源或同一普通光源的不同部分所发出的光是不相干的
那么如何获得相干光呢?
- 振幅分割法:薄膜干涉、牛顿环、迈克耳孙干涉仪
- 波阵面分割法:杨氏双缝干涉实验、劳埃德镜
干涉
杨氏双缝干涉实验

光程差:δ=dsinθ≈Ddx
当 δ 满足 δ=±kλ,k=0,1,2,⋯ 时,对应的条纹为明条纹。k=0 对应的条纹称为中央明纹。k=1,2,⋯ 对应的明条纹分别叫第一级、第二级……明条纹。
劳埃德镜
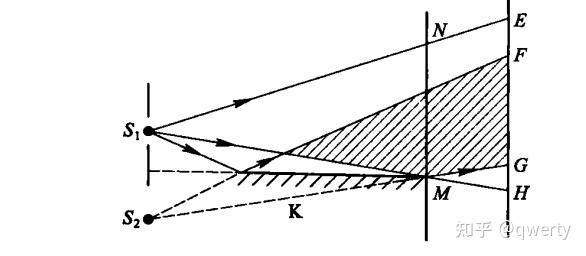
半波损失:光由光速较大的介质(光疏)射向光速较小的介质(光密)时,反射光相位突变 π
薄膜干涉
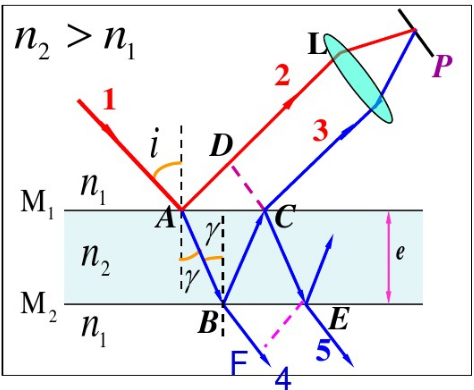
两束反射相干光的光程差:δ=2en22−n12sin2i+2λ
两束透射相干光的光程差:δ=2en22−n12sin2i
增透膜和增反膜
增透膜:对某一特定波长 λ,反射干涉相消,透过相长。
增反膜:对某一特定波长,反射干涉加强,使反射率大大加强,透射率相应减少。
等倾干涉

- 光程差取决于入射角
- 倾角 i 相同的光线对应同一级干涉条纹
- 膜变厚,条纹更密集;膜变薄,条纹更稀疏
劈尖干涉(等厚干涉)

牛顿环

光程差:δ=2nd+2λ
r≈2Rd=(δ−2λ)nR
明环半径:r=(k−21)nRλ,k=1,2,⋯
暗环半径:r=nkRλ,k=0,1,2,⋯
干涉图样:内疏外密、中心为暗点的圆环
迈克耳孙干涉仪
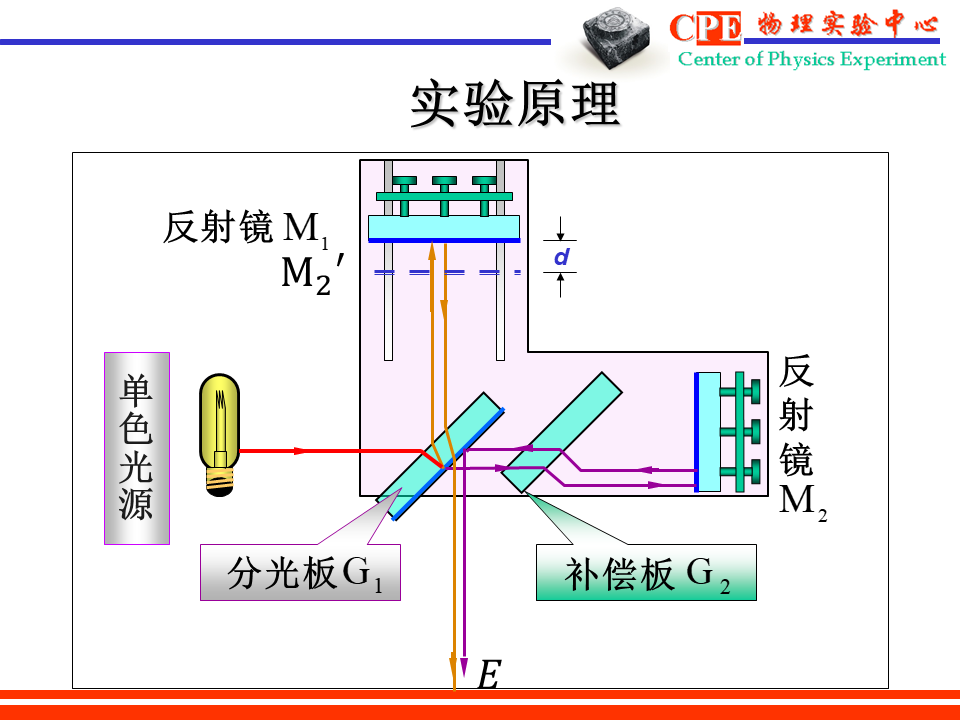
测出视场中移过的条纹数目 Δn,就可以算出 M1 移动的距离:
Δd=Δn2λ
衍射
夫琅禾费单缝衍射

暗条纹中心:bsinθ=±kλ,k=1,2,⋯
明条纹中心:bsinθ=±(2k+1)2λ,k=1,2,3,⋯
中央明纹宽度:Δx0=2bλf
其他任何两条相邻暗条纹(明条纹)宽度:Δx=bλf
夫琅禾费圆孔衍射
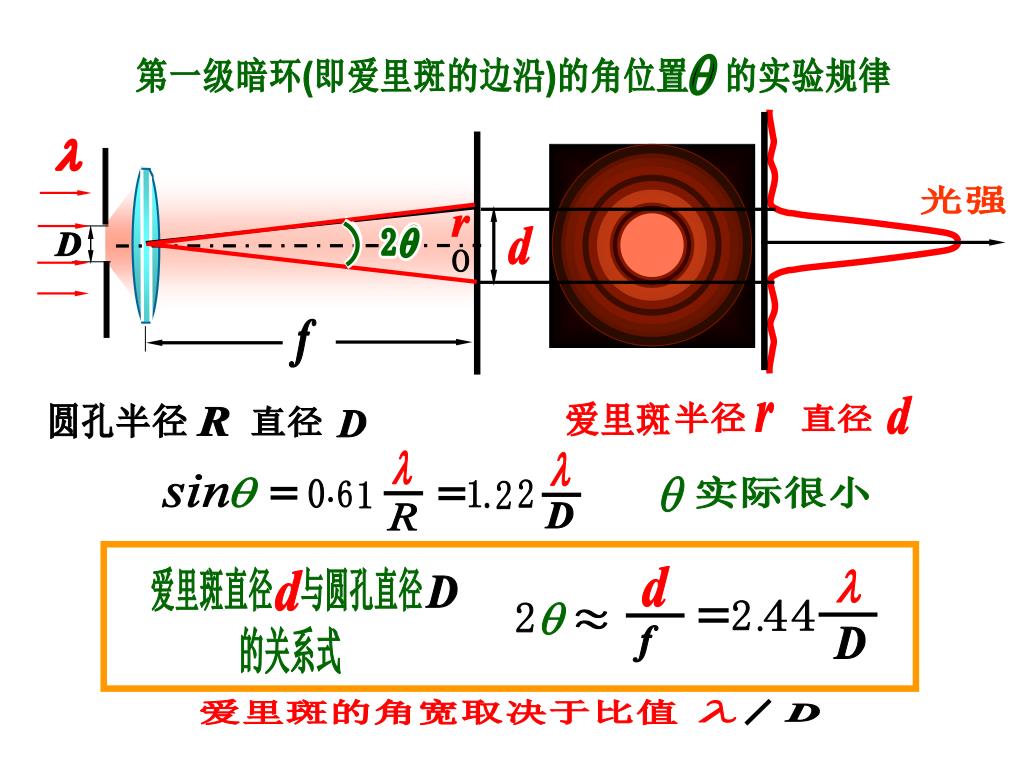
2θ=fd=2.44Dλ
最小分辨角:θ0=1.22Dλ
分辨本领:θ01
提高分辨本领的方法:增大透光孔径 D 或减小波长 λ
衍射光栅
光栅常量:d=b+b′
光栅衍射明条纹的条件:dsinθ=±kλ,k=0,1,2,⋯
k=0 的明纹称为中央明纹,k=1,2,⋯ 的明纹分别叫第一级、第二级、……明纹。
光栅中的狭缝条数越多,明纹就越亮越窄。
光栅衍射暗条纹的条件:dsinθ=±Nk′λ,k′=1,2,⋅,(N−1),(N+1),(N+2),⋯,(2N−1),⋯
次明纹:两相邻暗纹之间的明纹,光强远小于主明纹。
缺级现象
(b+b′)sinθ=±kλ,k=0,1,2,⋯bsinθ=±k′λ,k=1,2,⋯
两式相除
bb+b′=k′k
偏振
马吕斯定律
强度为 I0 的偏振光检偏器后,出射光的强度为 I0cos2α,其中 α 为起偏器和检偏器的夹角。
用该定律可以证明,强度为 I0 的自然光通过起偏器后,出射光的光强为 21I0
反射光和折射光的偏振
理论和实验都表明,当自然光入射到折射率分别为 n1 和 n2 的两种介质的分界面上时,反射光和折射光都是部分偏振光。其中反射光是垂直入射面的振动较强的部分偏振光,而折射光是平行入射面的振动较强的部分偏振光。
当入射角 iB 满足
taniB=n1n2
时,反射光为完全偏振光,且振动面垂直入射面,折射光为部分偏振光。此时,反射光和折射光互相垂直,把 iB 称为起偏角。








